
CHAPTER TWO: PROPORTION CHARTS
TABLE OF CONTENTS
from
How to Recognize When Special Causes Exist,
A Guide to Statistical Process Control
© Ends of the Earth Learning Group 1998
by
Linda Turner and Ron Turner
Proportion Charts are for those times when you need to
figure out what
percent of the time
something is occurring.
# failures
VS
# successes
# wins
VS
# losses
# correct
VS
# incorrect
You must know the number of times something was done
correctly and incorrectly in
order to use a "proportion-chart." |
- We won 57% of our games.
- Our absenteeism rate is 5% per day.
- 10% of our new hires will not make it even
one year.
- Our reject rate is 4% of all product.
- Our rework rate is 25%.
- The average student answers 40 questions
correctly on a 50 question test
- 10% of the time, our phone operators
forget to say, "Thank you for calling."
- We are using only 85% of our capacity.
- Last year, 750 of our customers bought
from us more than once.
- Our vendors sent the wrong things about 1
time out of a hundred last year.
- 22 employees said, "I hate it here."
|
"P-Charts" describe your data in terms of percents or fractions. "P-Charts" can be
used for any raw data which is either "right" or "wrong."
"np-Charts" are a
restricted version of "P-Charts" which track data in terms of number of failures per
subgroup rather than tracking failures as a percent of activity.
P-Charts describe activities in terms of proportions.
- We answered the phone within
three rings 80% of the time
- We made at least one or more errors
per piece of paperwork .05 of the
time.
There are no restrictions on
subgroup size when you use P-charts.
- My subgroup is one day's work.
We get a varying number of
phone calls every day, but the
average is about 95. The
subgroup size is "n."
- My subgroup is a week's worth
of paperwork. Our workload
varies over time from 800 pieces
of paperwork to 1000 pieces.
The average is about 900. The
subgroup size is "n."
|
np-charts describe activities in terms of
numbers.
- We failed to answer the phone
within three rings 23 times a day
- We made mistakes on 11 pieces
of paperwork per day
All your subgroups must be the same
size in order to use an np-chart.
- My subgroup is one day's work.
We get the same number of
phone calls every day, 95. The
subgroup size is "n."
- My subgroup is a week's worth
of paperwork. Our workload is
always the same, 900 pieces of
paperwork each week. The
subgroup size is "n."
|
Note: For those of you familiar with Deming's Red Bead Exercise, described in Out of the
Crisis, the formula he used was a type of an np-chart.
The following "example" shows how to create a "P-Chart" following a simple 12-step method.
***********************
ASSIGNMENT: Figure out how well a system for processing paperwork is functioning.
SIZE OF SUBGROUP: One day's work.
MEASUREMENT: Either the paperwork was a success meaning there were no mistakes
in it, or the paperwork was a failure which required rework due to one or more errors.
| In the table below, raw data has been collected in the first three columns. Based on this data, the values in "blue" are calculated in order to create a P-Chart. |
If the paperwork example doesn't fit
your work situation, then substitute for
"paperwork" whatever it is that you
do. |
DATA FOR P-CHART EXERCISE
Results from doing an average of 85 pieces of paperwork per day.
Subgroup
day |
# of paper forms
processed =
Opportunities |
# of forms with at least one error =
Failures |
# failures/
# opportunities =
% Failure |
| Day 1 |
93 |
25 |
26.9% |
| Day 2 |
85 |
17 |
20.0% |
| Day 3 |
85 |
18 |
21.2% |
| Day 4 |
87 |
23 |
26.4% |
| Day 5 |
86 |
15 |
17.4% |
| Day 6 |
85 |
15 |
17.6% |
| Day 7 |
88 |
16 |
18.2% |
| Day 8 |
97 |
12 |
12.4% |
| Day 9 |
80 |
12 |
15.0% |
| Day 10 |
85 |
13 |
15.5% |
| Day 11 |
69 |
23 |
33.3% |
| Day 12 |
84 |
12 |
14.3% |
| Day 13 |
82 |
11 |
13.4% |
| Day 14 |
85 |
18 |
21.2% |
| Day 15 |
76 |
12 |
15.8% |
| Day 16 |
86 |
18 |
20.9% |
| Day 17 |
91 |
17 |
18.7% |
| Day 18 |
89 |
22 |
24.7% |
| Day 19 |
82 |
22 |
26.8% |
| Day 20 |
86 |
19 |
22.1% |
| Total of 20
subgroups |
1700 |
340 |
20.0% |
|
|
|
|
| Average |
85 |
17 |
20.0% |
| Average Variance |
0.001882 |
| Average Sigma |
4.3% |
STEP #1: DO YOU HAVE ENOUGH DATA TO CREATE A
CHART?
|
Requirements
A. The average subgroup must
have a minimum of five successes and five
failures.
B. You need at least 20 subgroups |
Questions
A. How many are your average
number of successes and failures
per subgroup? Answer: The average number of failures was 17. Since there were 85 opportunities on average, that means there must have been 68 successes on average (85-17=68.)
B. How many subgroups do
you have? Answer: There are twenty days of data. | |
QUESTION: "What would you do if either of these conditions were not met?"
| ANSWER:
If the subgroup didn't have enough successes and failures,
then I would have to increase the subgroup size,
perhaps measuring workload by the
week (85 opportunities/day times 5
days/week would equal a subgroup
size of 440 pieces of paper.) In that
case, I would need 20 weeks instead
of 20 days worth of data.
|
ANSWER:
If I needed more subgroups, I would
patiently gather more data. In the meantime,
I could create a P-Chart, but I would caution
everyone to be extremely careful about using
the results prematurely. The reason 20
subgroups is required is that in experiments
it was found that using less than 20
subgroups frequently lead to misleading
central tendencies and control lines. | |
WARNING: If your system changes while in the midst of
gathering data, then you must start your count of 20
subgroups over again.
STEP #2: FIND THE CENTRAL TENDENCY
| Requirement: The central tendency is
the mean (traditional average)
percentage per day. It is labeled "p."
Choice: You can make your central tendency
either average percent failures or average percent successes.
In general, we recommend choosing average percent
failures.
|
What is the central tendency for percent failures for this data? Answer: 340 failures divided by 1700 opportunities = 20% failure rate.
| |
STEP #3: FIND THE AVERAGE SIZE OF A SUBGROUP
| The size of the variance and sigma depend upon how large the subgroup is. For instance, the sigma for Day 1 with 93 opportunities will be smaller than the sigma for Day 2 with 85 opportunities. In order to simplify appearances, the average subgroup can be used instead of calculating a separate sigma for every subgroup. |
What is the average size of a subgroup? Answer: 1700 opportunities divided by 20 subgroups = 85 opportunities on average.
| |
STEP #4: FIND THE VARIANCE FOR THE AVERAGE
SUBGROUP SIZE
|
Requirement: The formula for
variance is:
V = p(100%-p)/n
The variance is equal to the percent failures
times the percent successes divided by the size
of the subgroup |
V = variance
p = central tendency (% failures)
(100%-p) = % successes
n = size of the subgroups
V = (20%) (80%) / 85 = .001882
|
|
|
What is variance?
Variance and standard deviation measure how much variation exists within a set of data. In general, the bigger the variance, the greater the range between high and low values, and the greater the overall variation. Sometimes, newcomers to SPC have taken some statistics courses along the way and were taught a different formula for variance than the formulas used in SPC. They
always want to know, "Why the difference?"
The reason for the difference is that the classic formula for variance measures how much variation there is in the raw data itself, whereas SPC variance measures how much variation we should expect assuming there are no special causes in the data. For instance, if all subgroups had an identical percent failure of 20%, then variance for the raw data would be zero since there would be no variation in their results. SPC variance, though, would be the same .001882 we calculated above. Our eight rules for identifying specialness would then compare the raw data to what should be expected from normal variation. If all raw data results were identical, we would conclude using Rule 7 that something "special" is going on.
If this doesn't make any sense to you, don't worry about it, and go on faith that the mathematicians know what they are talking about.
Note: Sometimes variance is symbolized by S2 instead of by V. | |
STEP #5: FIND SIGMA (THE STANDARD DEVIATION):
Sigma is the square root of the variance. |
Sigma is the square root of .001882 or .043382 which equals about 4.3%. | |
STEP#6: FIND THE ONE SIGMA LINES
| The Upper One-Sigma Line is the
central tendency plus sigma. The Lower One-Sigma Line is the
central tendency less sigma |
The Upper One Sigma Line is 20.0%+4.3% = 24.3% The Lower One Sigma Line is 20.0%-4.3% = 15.7%
| |
STEP #7: FIND THE WARNING LINES:
The Upper Warning Line (UWL) is the
central tendency plus 2 sigma. The Lower Warning Line (LWL) is the
central tendency less 2 sigma. |
UWL = 20.0% + (2)(4.3382 %) = 28.7%
LWL = 20.0% - (2)(4.3382%) = 11.3%.
| |
STEP #8: FIND THE CONTROL LINES:
The Upper Control Line (UCL) is the
central tendency plus 3 sigma. The Lower Control Line (LCL) is the
central tendency less 3 sigma. |
The UCL is 20.0% + (3)(4.3382%) = 33.0%.
The LCL is 20.0% - (3)(4.3382%) = 7.0%.
Note: if you rounded your sigma off to 4.3% and used that number to calculate warning and control lines, you would get slightly different results that usually are not significant.
|
|
STEP #9: CREATE AN SPC CHART
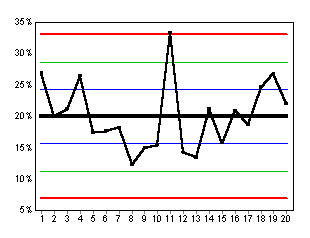 |
A. The vertical axis measures "Percent Failures." The horizontal axis tracks data by the subgroup day.
B. The red lines are the control lines. The green lines are the warning lines. The blue lines are the one-sigma lines.
C. The daily average failure rate is drawn in black.
|
STEP #10: APPLY THE EIGHT RULES FOR
IDENTIFYING SPECIALNESS
|
1. Any values outside the control lines. Freak value
2. Two out of three points in a row in the
region beyond a single warning line. Freak value
3. Six points in a row steadily increasing or
decreasing. Process shift
4. Nine points in a row on just one side of
the central tendency. Process shift
5. Four out of five points in a row in the
region beyond a single one-sigma line.Process shift
6. Fourteen points in a row which alternate
directions. Shift work or overcorrection
7. Fifteen points in a row within the region
bounded by plus or minus one sigma. Garbage data or overcorrection
8. Eight points in a row all outside the region
bounded by plus or minus one sigma. Garbage data or overcorrection
| Only Day 11 appears special. In Step #11, the adjustment will rule out specialness even for Day 11. |
|
STEP #11: ADJUST FOR SUBGROUPS WHOSE SIZES ARE SIGNIFICANTLY DIFFERENT THAN THE AVERAGE SUBGROUP
If you examine the equation for the Variance [ V = p(100%-p)/n ], you will notice that variance is dependent upon "n", the number of opportunities in a given
subgroup. Higher "n" values will mean lower variances and standard deviations.
The rule of thumb is this: if you quadruple your "n", the variance will be reduced to one-quarter of its initial value and the standard deviation will be halved. This in turn will make the gap between control lines to come closer by half.
If you look at Day 11, you will discover that not only does it have the highest failure rate (at 33.0%), but it also has the smallest number of opportunities to goof. The smallest "n" of 69 opportunities (compared to the average of 85) means that we should recalculate sigma for this day since our control lines will be farther apart than before.
Computer SPC programs do this automatically for you. The resulting control lines step in and out based on how large the "n" is for each day. For Day 11, for instance, the variance and standard deviation would be:
Variance = (p)(100%-p)/n = (20%)(80%)/69 = .002319
Sigma = the square root of .002319 = .048154 = 4.8154%
The Upper Control Line would be 20% + 3(4.8154%) = 34.4%
The original Upper Control Line was 33.0% which was below Day 11's value of 33.3%. Once we take into account the number of opportunities though, we discover that Day 11 was in fact not special and should not be investigated. The graph below shows this.
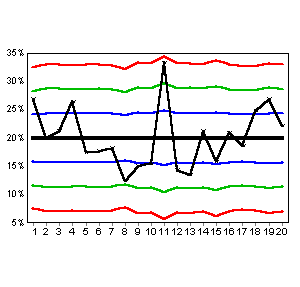 |
The control lines "step" in and out based on the number of opportunities. A larger "n" means closer lines. Day 11 now appears inside the Control Lines once the smaller "n" is taken into account. Day 8 had the most opportunities of any day. Correspondingly its control lines are closest of any day.
|
Intuitively if we flipped a fair coin with a 50% chance of getting heads, out of ten flips, we would expect to get about 5 heads. No one would think it odd to be off 20% either way though and in fact getting only 3 heads or getting 7 heads would not indicate that anyone cheated or that other special causes were happening.
If we flipped the coin 1000 times though, being off by 20% would be very odd and grounds for suspecting a special cause was at work. In fact, with a thousand flips, being off by 5% (at 55% or 45% heads) would be grounds for investigating special causes.
In the same manner, as each subgroup has more data with which to work, the control lines become closer and we can better judge when a special cause is occurring.
STEP #12: REMOVE ANY SUBGROUPS THAT HAVE "SPECIAL CAUSES" AND RECALCULATE THE CENTRAL TENDENCY AND SIGMA.
Subgroups that have special causes are by definition not part of a stable process. Remove them from your data base and recalculate the central tendency and control lines. Usually this causes the control lines to come closer together. It is conceivable that after recalculating them, more subgroups will fall into a "special" category in which case you would repeat step #12.
Since there were no special days in this data base, no recalculation is necessary.
Unfortunately most computer SPC programs do not automatically do Step #12 for you. In these cases, you will manually have to remove the special-cause data and then recalculate your lines.
NP-CHARTS
There are differing forms of proportion charts which are used when the number of opportunities in a subgroup remain constant. For instance, you might track the number of failures per batch of 100 pieces of paperwork. Or if on any given day, you always did 85 pieces of paperwork, then you could use an np-chart in which the subgroup was a day's work.
The letter "n" refers to the number of opporunities in a subgroup while the letter "p" refers to the proportion of failures. If for instance, "n" had been 85 and "p" had been 20%, then "np" would be 17.
For an np-Chart, the central tendency is "np".
The variance is np(100%-p). In words, the "variance is the average number of failures times the average success rate." If "np" was 17 and the failure rate was 20%, then the variance would be 17(80%) = 13.6.
Sigma or the standard deviation is again the square root of the variance. If the variance was 13.6, sigma would be 3.7.
The One-Sigma Lines for this example would be at 17 plus or minus 3.7 (yielding 20.7 and 13.3).
The Warning Lines would be at 17 plus or minus 2 times 3.7 (yielding 24.4 and 19.6.)
The Contol Lines would be at plus or minus 3 sigma (yielding 28.1 and 15.9.)
COMPARISON BETWEEN P-CHARTS AND NP-CHARTS:
If you look at the Day 2 data above, there were 85 opportunities and 17 failures. If we had created an "np-chart", then the "data point" would be 17 failures instead of 20.0%. The Upper Control Line for the P-Chart was 33.0%. If you multiply this 33.0% times 85 opportunities, you will get 28.1 failures or the same Upper Control Line you would have gotten using the np-Chart method. The only advantage of the "np-Chart" method is that it is easier for some people to think in terms of actual count of errors rather than in percents. The disadvantage of the "np-Chart" method is that it requires that the number of opportunities be the same every day.
|
APPENDIX A: "TIPS" SPC Charts are best used on an ongoing basis so that you can identify as quickly as possible when something special is going on. The paperwork example we used in this chapter would have you track your results daily, probably first thing in the morning.
If the errors you discover were made weeks earlier, then diagnostics as to what was the underlying "special" cause of problems will be quite problematic. Speeding up detection of errors is a basic systems principle which will dramatically improve overall functioning. (We discuss this in How To Blame The System And Not Mean, "I Give Up!" 14 Principles For Improving Systems)
One way to speed-up detection of specialness is to track data in smaller subgroups. If for example, we tracked data by the half-day, then clearly we might more quickly detect when something has gone out of control. We would also attain our needed twenty data elements in only 10 days instead of 20.
For instance, Day 4 in our original data set had 23 failures out of 87 opportunities for a 26.4% failure rate, clearly within normal variation. Assume the day was divided into a morning shift, which had 16 failures out of 40 opportunities (for a 40% failure rate), and an afternoon shift, which had 7 failures out of 45 opportunities (for a 15% failure rate.) We would need to recalculate the Upper Control Line using the smaller sized subgroup for the morning (40 instead of 87 for the day). In this case, the variance for the morning would be (20%)(80%)/40 which is .004000. Sigma would be 6.3246%. The Upper Control Line would be 39%. Clearly the morning (at 40%) was "special". We would have missed this using the larger day-long subgroup. Similarly the afternoon at 15% would not be special because the Lower Control Line would be only 2.5%.
There is a limit to how small your subgroups can be made. We must have an average of at least 5 failures per subgroup. In the case of our paperwork example, that would mean that the smallest average subgroup size we could have would be 25 opportunities (since 20% of 25 is five failures.) That means we could not break our day into quarters since each quarter would average only 21-22 opportunties.
As your processes improve and failure rates fall, this will mean that your subgroup sizes must be increased. For instance, if our paperwork failure rate was 10% instead of 20%, then our minimum subgroup size would be 50 (since 10% of 50 would be five failures.) You could no longer track data by the half day. If our failure rate fell to 5%, then our minimum average subgroup size would need to increase to 100 opportunities. In this case, we would have to have subgroups larger than one day's work.
Generally speaking, as you reduce your overall failure rate, there will start being fewer and fewer special causes at work. Improvements therefore will increasingly start coming from fundamental system improvements rather than by focusing on "fixing" special cause situations.
Lastly, mark on your SPC Charts any changes you are making. If you have made system improvements, draw a vertical line that corresponds to the day on which you made the changes. Track data for 20 subgroups. If the average failure rate has dropped (or worsened) over that time period, then re-calculate your central tendency and control lines to represent the change.
| |
|
APPENDIX B: WHY DOES SPC WORK? This is not required reading, but will explain the theory behind SPC Charts for those of you who want a deeper understanding.
Unfortunately we have to start our explanation with a review of some basic statistics vocabulary.
Distributions: A distribution refers to a set of data. In our example for this chapter, we could talk about the distribution for Day 2 or we could talk about the distribution for all 20 days.
Frequency Distribution: When the data within a distribution is tracked by how frequently different values occur, this is called a frequency distribution. Below the number of failures and successes from our sample data above is tracked in a frequency distribution.
| Frequency |
| 1700 (100%) |
---- |
---- |
| 1360 (80%) |
xxxx |
---- |
| 1020 (60%) |
xxxx |
---- |
| 680 (40%) |
xxxx |
---- |
| 340 (20%) |
xxxx |
xxxx |
|
successes |
failures |
Binomial Distributions: Don't let the jargon scare you off. This kind of distribution simply means that we limit our choice of values to two possibilities. If we graphed the example data in terms of successes and failures, we would have two columns in which the frequency for successes would be 1360 (or 80%) and the frequency of failures would be 340 (or 20%).
With this data, we would know the mean (average) is 20% failure. The above frequency distribution is binomial.
Normal Distributions (and Curves): By connecting the tops of each column in a frequency distribution, we can create a "curve" that describes that distribution. Normal distributions are symmetric about the mean. If you roll two dice, you have a possibility of getting anything from 2 to 12. The mean roll will be 7. The frequency with which you roll 2s will probably be the same as the frequency with which you roll 12s.
Normal distributions have the same shape as a sideways view of a bell. For that reason normal distributions are also called bell-shaped distributions. Statisticians have extensively studied normal distributions and can tell you many details about the data in such a distribution simply by knowing the mean (average) and the standard deviation (sigma.) For instance, we know for any normal distribution that 2/3 of its values will usually be between plus and minus one sigma from the mean. All of our SPC Rules require that the underlying distribution be normal.
The binomial distribution above is clearly NOT normal.
The Central Limit Theorem: This theorem is critical for SPC because it makes it possible to convert any set of raw data into a normal distribution. The Central Limit Theorem allows us to do this:
- Break a set of data into smaller subgroups. In the chapter example we took the twenty days worth of data and broke it into 20 subgroups.
- Find the mean (average) for each of the subgroups. This is what we did when we came up with the failure rate per subgroup.
- Create a new distribution of these averages. Instead of dealing with the original binomial distribution, we instead created charts that included the average failure rate for each day.
- The resulting distribution of averages will approximate a normal distribution.
The Central Limit Theorem says that in theory, distributions of subgroup averages will appear to be closer and closer to a normal distribution as more subgroups are added to the data base. The Theorem doesn't say how many subgroups are necessary. Walter Shewhart set up experiments in which he tried various numbers of subgroups in order to see at what point the distribution started to look normal. For five or fewer subgroups, normalcy was frequently difficult to see. It wasn't until 20 subgroups or more were included in the data base that the distribution started to appear "normal". Based on Shewhart's experiments, the requirement for having 20 subgroups was developed.
NORMAL DISTRIBUTION

| The Normal Curve or Bell Curve is symmetrical about the mean. When raw data is converted into subgroups, then the averages of the subgroup will always form a Normal Curve around the grand average of every subgroup. This "normal variation" then becomes our statistical expectation as long as the system has remained stable without process shifts or other special causes. |
Finding "specialness." When we say that a process is "in control," that means the process has a stable "mean" and "standard deviation." In the example for this chapter, the mean failure rate for the data was 20%. That means for each subgroup, we would expect to get about 20% failures, but just due to luck, we would expect sometimes to get higher or lower scores. We then compare our expectations (assuming there is a stable 20% failure rate) with the reality. If the difference is great enough, we then say, "something special was going on during certain of the subgroups."
Freak values. When the process gets an extreme high or low and then returns to normal, we call this a freak value. Freak values include any values outside the control lines. Usually there is a very ready explanation for such freak scores. If you want to make your SPC Chart more sensitive to freak values, then you have to make your subgroup size bigger. This will cause sigma to decrease and your control lines to get closer together. For instance using our chapter data, if you doubled the average subgroup size from 85 to 170, then sigma would drop from 4.3% to 3.1%. The Upper Control Line would then shift from 33.0% to 29.2%. Unfortunately, the price for making the subgroup bigger is that you have to wait twice as long in order to get sufficient data. Of our eight rules for identifying specialness, the first two are most likely to identify freak values.
Process shifts. A process shift indicates that the long term average has changed either for the better or worse. Unless the process shifts quite dramatically, you won't at first be aware that things have changed. Of our eight rules, Rules #3 through #6 are best for identifying process shifts.
| |

TABLE OF CONTENTS




